1.2 Contact angle, wetting, and spreading 

The surface tension of solids, especially polymers with a low surface free energy cannot be measured directly because of the elastic and viscous restraints of the bulk phase, which necessitates the use of indirect methods. The mobility of the surface molecules in a solid is exceedingly low when compared with any liquid, and a solid surface does not usually display those faces demanded by the macroscopic minimizing of surface free energy. Most solids are incapable of adjusting to such equilibrium conformations and in practice their surface structure will be largely a frozen-in record of an arbitrary past history, where some imperfections, humps and cracks are present. Thus, the laws of capillarity of liquids cannot be applied to solids. The only general method is the rather empirical method of estimating the solid surface tension from that of the contacting liquid.  

If we consider a liquid drop resting on a solid surface as shown in Figure 1.5, the drop is in equilibrium by balancing three forces, namely, the interfacial tensions between solid and liquid, SL; between solid and vapor, SV; and between liquid and vapor, LV. The contact angle, θ, is the angle formed by a liquid drop at the three-phase boundary where a liquid, gas and solid intersect, and it is included between the tangent plane to the surface of the liquid and the tangent plane to the surface of the solid, at the point of intersection. The contact angle is a quantitative measure of the wetting of a solid by a liquid. Unless it is very volatile, any liquid (including liquid metals such as mercury) having a low viscosity can be used as the liquid of the drop. The contact angle is usually measured on the liquid side (when the system involves two liquids, it is usually measured on the denser liquid side).

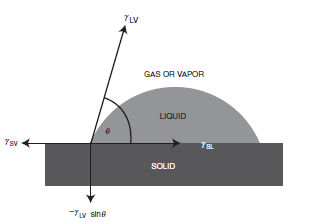
Fig. 1.5 Vectorial equilibrium for a drop of a liquid resting on a solid surface to balance three forces, namely, the interfacial tensions, between solid and liquid, γ_SL, that between solid and vapor, γ_SV, and that between liquid and vapor, γLV, resulting in Young’s equation: (γSV = γSL + γLV cosθ), where q is the contact angle. The down component of the vector forces (−γLV sinθ) is also shown.

The largest observed value for water on a smooth solid surface at equilibrium is about 160°(Lotus leaf and spider legs).

The position of the triple interface will change in response to the horizontal components of the interfacial tensions acting on it. T. Young [1] was the first to describe contact angle equilibrium, in 1805. The vectorial summation of forces at the three-phase intersection point (the so-called three-phase contact point) gives: 

γ _GS = γ _LS + γ _GL cosθ.                                                                                                                                              (1.2)  

where  γ is the surface tension (or surface free energy) term. If [γ _SV > (γ _SL +γ _LV)] which shows the presence of a high surface energy solid, then Young’s equation indicates (cosθ = 1), corresponding to (θ = 0), which means the complete spreading of the liquid on this solid. On the other hand, in order to complete the resolution of vector forces about the three-phase contact point, an up component (γ_LVsinθ) should be present, as shown in Figure 1.5. This force is balanced with a (−γ_LVsinθ) force that corresponds to the strain field on the surface of the solid. It is shown that this strain causes the formation of micro humps on the surface of some soft polymers when a strongly interacting liquid drop (giving low q values) sits on them.However, when the drop is initially placed on the surface the interfacial tensions will not be in equilibrium. The net force per unit length of the triple interface along the solid surface will then be: 

F _h = γ_VS − γ_LS – γ_VL cosθ′                                                      (1.3)

Where forces acting to the right are given positive signs and those acting to the left have negative signs. The angle θ′ is the instantaneous contact angle and will change as the triple interface moves towards its equilibrium position where θ′ =θ and F_h = 0.

Although Eqn 1.2 describes the equilibrium contact angle in terms of the interfacial tensions involved, it gives no real insight into the reason that a certain value of contact angle is reached. We observe that some surfaces have a very high contact angle for water, while for others it is so low as to be immeasurable. An understanding of the origin of contact angle requires knowledge of the balance of forces between molecules in the liquid drop (cohesive forces), and those between the liquid molecules and the surface (adhesive forces). A surface that has primarily polar groups on the surface, such as hydroxyl groups, will have a good affinity for water and, therefore, strong adhesive forces and a low contact angle. Such a surface is called hydrophilic. If the surface is made up of non-polar groups, which is common for polymer surfaces or surfaces covered by an organic layer, we say that the surface is hydrophobic, and the contact angle will be large. Hygrophilic and hygrophobic literally mean liquid-loving and liquid-fearing, and in case of water in air, the terms hydrophilic and hydrophobic are used. It follows that measurements of contact angle are frequently used as a quick and simple method to gain qualitative information about the chemical nature of the surface. More generally, the terms appropriate for all liquids are lyophilic and lyophobic(solvent loving and solvent hating). 

Many surfaces show an apparent hysteresis, where different values of the contact angle are measured depending on whether the measurement is performed on a drop of increasing size (the advancing contact angle) or of diminishing size (the receding contact angle). This is normally due to roughness of the surface, and the difference between advancing and receding contact angles is another useful and quick method of gaining qualitative information about the nature of the surface. Although the macroscopic observation of angles shows hysteresis, it is likely that the microscopic angles, if they could be observed, would show no hysteresis. The advancing contact angle (liquid moving over an apparently dry surface) is greater than the receding angle, thus when a contact angle close to zero is needed, as for example when surface tension is to be measured by a Wilhelmy plate method [2], the surface of the solid is often roughened and a receding contact angle used. 

Contact angle measurements are made by placing a drop of the liquid on a surface and viewing it with some type of magnifying lens (Figure 1.6). The angle can then be measured optically, usually by taking a digital image and using software to determine the angle. The most difficult part of dealing with very high contact angles (super-hydrophobic) is keeping the drops in place long enough to be measured! The slightest tilt on the surface is enough to cause the drops to roll off.

Fig. 1.6 A contact angle image showing a drop of water on a PTFE surface. The needle used to deposit the drop is visible at the top.

Wetting is determined by the equilibrium contact angle, θ. Low values of θ indicate a strong liquid–solid interaction such that the liquid tends to spread on the solid, or wets well, while high θ values indicate weak interaction and poor wetting. If θ  is less than 90°, then the liquid is said to wet (or sometimes partially wet) the solid. A zero contact angle (θ = 0) represents complete or perfect wetting. If θ is greater than 90°, then it is said to be non-wetting. Contact angles of 180° are not found, as there is always some interaction between the liquid and the solid. From a microscopic point of view, if the solid has a low-energy surface, it attracts the molecules of the liquid with less force than the liquid molecules attract one another. Therefore, the molecules in the liquid next to the surface have a weaker force field than in the liquid surface, so that the liquid molecules at the interface are pulled more strongly into the bulk of the liquid than they are by the solid. There is a tension in the layer adjacent to the solid, and the liquid molecules are somewhat separated, owing to the one-sided force field. The situation is analogous to the behavior of a drop of one liquid on another immiscible liquid, the drop liquid having a higher surface tension than that of the lower liquid (but not equivalent because of the mobility of surface molecules at the interphase region between two immiscible liquids).

The spreading of a liquid over a solid depends on the components of the interfacial tensions acting parallel to the solid surface at the line of contact, as in Eq. (1.3). The triple interface will move in the direction dictated by F_h until a value of θ is reached at which F_h = 0, giving equilibrium, or, if such a position is not possible, the liquid spreads completely, and then θ’= 0, cosθ’ = 1, and Eq. (1.3) becomes:

       F_h(θ′ = 0) = γ_VS − γ_LS − γ_VL .                                                                                                      (1.4) 

It is convenient to define a spreading coefficient, S_LS, by

      S_LS = γ _VS − γ _LS − γ _VL.                                                                                                            (1.5)

If S_LS > 0, the liquid spreads completely, whereas if S_LS ≤ 0 the drop does not spread completely and it finds an equilibrium contact angle, θ^eq, where F_h = 0.