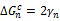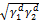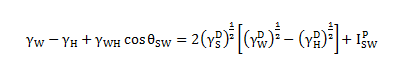Measurement of contact angles on solids yields data that reflect the thermodynamics of a liquid/solid interaction. These data can be used to estimate the surface tension of the solid. For this purpose, drops of a series of liquids are formed on the solid surface and their contact angles are measured. Calculations based on these measurements produce a parameter (critical surface tension, surface tension, surface free energy etc.), which quantifies the characteristic of the solid surface and its wettability.

3.1Thermodynamic formula

3.1.1 Berthelot’s combining rule

Brethelot [44] used the geometric mean combining rule for the first time in obtaining the interfacial tension from the surface tensions of the two phases. The relationship was based on the way dispersion energy coefficients C₆^{i j} can be written in terms of C₆ⁱⁱ and C₆^{j j} in the treatment of London theory of dispersion forces:

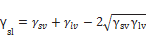              (1.33)

This relation forms the basis of the Berthelot combining rule [Eq. 1.34] where ε_ij is the potential parameter (well depth) of unlike-pair interactions, ε_ii and ε_jj are he potential energy parameters (well depth) of like-pair interactions [45]

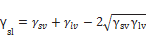        (1.34)

This equation was written in terms of work of adhesion between two phases (i.e. W_sl ) and work of cohesion of the two phases (i.e. W_ss and W_ll).

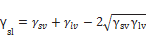                                                               (1.35)

Putting the relevant values, i.e. W_ss=2γ_sv , W_{l l}= 2γ_LV and W_sl=γ_LV +γ_sv -γ_sL in Eq. 1.35 and rearranging we get the final relation of Berthelot:

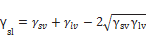        (1.36)

3.1.2 Antonow’s rule

Brethelot [44] used the geometric mean combining rule for the first time in obtaining the interfacial tension from the surface tensions of the two phases. The relationship was based on the way dispersion energy coefficients C₆^{i j} can be written in terms of C₆ⁱⁱ and C₆^{j j} in the treatment of London theory of dispersion forces:

In 1907 Antonow [46] related γSL in terms of γSV and γLV in a simple manner as in Eq. 1.36. There was no theoretical background behind this relationship according to Kwok and Neumann [45].

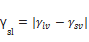           (1.37)

3.2 Thermodynamic approaches for the estimation of Surface free energy of solid.

In the literature, various different approaches were mentioned which makes it possible to evaluate the solid surface tension using measured contact angles by liquids with known or pre-characterised surface energy parameters.

Fig. 1.14 Theoretical estimation of the possibility and extent of microbial adhesion on solid surfaces. Approaches to convert contact angle data into solid surface energy. 

Fig. 1.15 Chronological development of different approaches for evaluation of surface energy of solids from contact angle goniometry.

3.2.1 Zisman critical surface tension

Following the influence of Thompson [47,48] and Gibbs [49], Zisman and coworkers [50] made pioneering investigations of the thermodynamics of wetting and adhesion.

Let us recall that Eqns. 1.2 and 1.12 are the basic thermodynamic equations describing the relation between surface free energy and wetting. These equations might be rewritten to clarify the present argument in the following way.

          (1.38)

           (1.39)

where the subscript LV⁰ refers to liquid-saturated vapor interface, SV⁰ is the solid saturated with vapor interface and S⁰ is the solid interface in absence of liquid vapor. From Eqns. 1.38 and 1.39 it follows that:

      (1.40)

where

              (1.41)

here  is the surface excess (amount adsorbed) of the liquid vapor and P⁰ the saturation vapor pressure of liquid phase. The vapor is assumed to be ideal. Also note that Eqn. 1.39 reduces to Eqn. 1.12 when the film pressure, ne, approaches zero. For low surface free energy solids 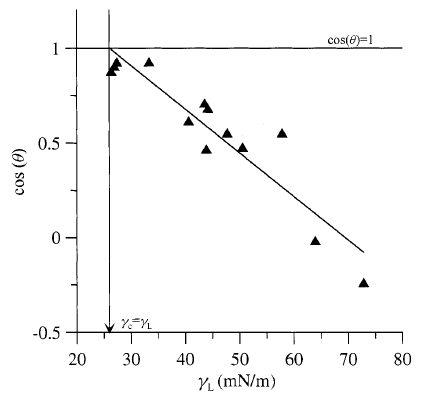 = 0.

Zisman and co-workers also noted that plots of cos(θ) vs.  were nearly linear, particularly when homologous series of liquids were used. It thus follows that:

        (1.42)

where  γc is referred to as the Zisman critical surface tension. A plot of cos(θ) vs. γ_LV⁰ will intersect cos(θ)= 1 when γ_LV⁰ =γ_c, (see Fig. 1.16). Zisman's relation is empirical.

From Eqn. 1.38 it can be seen that:

             (1.43)

Despite the fact that γ_c is not the solid surface free energy, the critical surface tension has been shown to correlate with the known surface chemistry of several solids. Determination of γ_c, is an adequate measure of solid surface free energy for many practical problems. Little information on the underlying surface is, however, learned.

Fig. 1.16 A Zisman plot. The critical surface tension is found where the linear fit to the data intersects cos (θ) = 1 and is about 26 mN/lm in this instance.

his approach has been extensively used to determine the critical surface tension γ_c of various low energy solids and organic films deposited on high energy solids like glass and metals. In general, a rectilinear relation is established empirically between the cosine of the contact angle and the liquid surface tension, for each homologous series of organic liquids . Fig. 1.17a illustrates the results with the n-alkanes or polytetrafluoroethylene. Even when cosθ is plotted against γ_LV⁰  for a variety of non-homologous liquids, the results fall close to a straight line or collect around it in a narrow band like that shown in Fig. 1.17b. certain low energy solids exhibit curvature of this band for liquids with surface tension above 50 mN/m (Fig. 1.17c), this results because weak hydrogen bonds form between the molecules of liquid and those in the solid. This is most likely to happen with liquids of high surface tension, because they are always hydrogen bond forming liquids (polar liquids). If critical surface tension is considered to give an indication of the surface tension of the solid then by using this method:

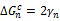
Fig. 1.17 (a) Wettability of polytetrafluoroethylene (Teflon) by n-alkanes; (b) wettability by various liquids on the surface of polyvenylchloride; and (c) wettability of polytetrafluoroethylene (Teflon) byvarious liquids. Taken from [51]

- it is possible to obtain the total solid surface energy of an apolar solid by using series of homologous apolar liquids, e.g. n-alkanes;

- it is possible to find only the dispersion force component γ_s^d . of the total surface energy of a polar solid by using series of homologous apolar liquids, e.g. n-alkanes, and;

- deviation from rectilinear relation is observed when polar liquids are used on polar and apolar solids by using the Zisman method. Hence, it is not possible to determine any component of the solid surface tension by using polar liquids using the Zisman method.

3.2.2 Good and Garifalco approach [52]

Accepting the Berthelot relation for the attractive constants between molecules, A_aa and A_bb, and between unlike molecules A_ab, i.e.

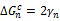       (1.43)

the authors arrived at an almost similar relationship as Brethelot but with a constantΦ.

Taking analogy from Eq. 1.43. they set up the corresponding ratio, involving the energies (or free energy) of adhesion and cohesion of two phases which was taken to equal a constant Φ:

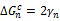      (1.44)

Using free energy of adhesion 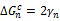and free energy of cohesion 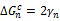, the following relation was attained:

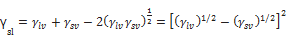                                                     (1.45)

and Φ was evaluated for different systems.

The value of Φ was found to be 1 for ‘regular’ interfaces, i.e. systems for which the cohesive forces of the two phases and the adhesive forces across the interface are of the same type. 

When the predominant forces within the separate phases are unlike, e.g. London -van der Waals vs. metallic or ionic or dipolar, then low values of Φ are expected. Clearly this applies to pairs such as non-hydrogen bonding in organic compound vs. water; organic compound vs. metal and salt vs. metal.

When there are specific interactions between the molecules forming the two phases, the energy of adhesion is greater than the value it should have in the absence of specific interactions.

3.2.3 Neumann ’s approach [53-63] (Equation of state)

Neumann and co-workers have discussed the surface tension of solids from a purely thermodynamic point of view. Their view contrasts with the statistical thermodynamic approaches used by van Oss, Chaudhury and Good, Chang- Chen and Fowkes (see earlier sections for references). Because the Neumann’s approach does not consider the molecular origins of surface tension no statistical mechanical insight is gained.

Kwok and Neumann [53] correctly remind us that that contact angle measurements can be difficult. Measured contact angles can deviate from the true Young's contact angle which satisfies Eqn.1.2. Both surface topography and surface chemical heterogeneity can affect the measured value for contact angle [64-67]. Grundke et al. [68] have recently discussed wetting on rough surfaces.

All of the thermodynamic approaches to calculate surface free energy which are explored in this paper assume that the following conditions apply:

- Young's equation is valid.

- Probe liquids are pure compounds. Mixtures are likely to exhibit selective surface adsorption (see, e.g., Adamson [book 1]).

- The surface tensions of materials are independent of the test conditions at fixed T and P (i.e., the surface tension of a solid is not modified by the probe liquid).

- γl >γ_s according to Neumann or more generally cos (θ) > 0 .

- γ_SV  is not influenced by liquids.

According to Kwok and Neumann [53], the contact angle can be expressed as a function of γ_lv and γ_SV only. Thus,

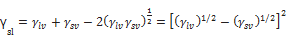           (1.46)

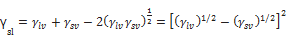         (1.47)

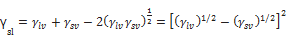    (1.48)

Where and F are suitable functions. Kwok and Neumann have observed smooth monotonic dependence of  with  consistent with Eqn. 1.46 when liquid-solid pairs conform closely to the assumptions listed above. For arbitrary solid-liquid pairs such a plot may show considerable scatter because the measured contact angles deviate significantly from the true Young's contact angle. Stick / slip behavior in advancing contact angles, time-dependent contact angles and liquid-surface tension changes during the course of the experiments result from physico-chemical interactions not consistent with the use of Young's equation for determining surface free energies.

The function, F, in Eqn. 1.48 has been historically modeled in several ways. Antonow [46] (recall Eqn.1.37, for instance) stated that:

        

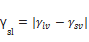
or combining with Young's equation

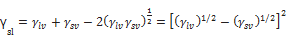             (1.50)

Alternatively, Berthelot’s rule (recall Eqn. 1.33, for instance) has been used such that

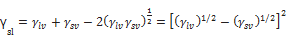        (1.51)

and again combining with Young’s equation

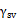       (1.52)

Eqn. 1.53 would be identical to that used in the van Oss, Chaudhury and Good model if the solid and liquid had only Lifshitz-van der Waals interactions such that If Eqns. 1.46 and 1.48 were adequate descriptors, then calculated values for  would be independent of the choice of probe liquid used. This is unfortunately not the case. Li and Neumann [63] have considered a modified Berthelot equation such that

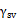       (1.53)

And 

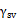       (1.54)

Empirically it has been shown that

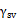        (1.55)

and that the measured solid surface free energy using this choice for β is nearly independent of the choice of liquid. Eqn. 1.43 can be used in two ways. First, β can be chosen from Eqn.1.44 and a suitable contact angle can be used to determine 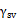 . Second, β and  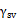  can be treated as adjustable parameters. Least-squares analysis using contact angles measured for several liquids is then used to determine the best fit values for β and 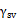   . The second approach would seem to be preferable.

An alternate combining rule has been suggested recently by Kwok and Neumann  [69]. It was a further modification of the Berthelot hypothesis:

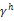          (1.56)

And β in this equation has been determined experimentally.

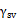        (1.55)

Kwok and Neumann [53] have criticized the van Oss, Chaudhury and Good approach for several reasons. The reasons include at least the following:

- The Neumann model uses fewer adjustable parameters; two versus six

- Surface free energies measured using the van Oss, Chaudhury and Good may appear to depend on the choice of liquids

- The assigned values for the van Oss, Chaudhury and Good parameters are assigned in ways not fully satisfactory to Neumann and co-workers.

It is my opinion that Kwok and Neumann have properly identified experimental factors that result in significant deviations of measured contact angles from the true Young’s contact angle. Application of any of the above models requires that Young’s equation be valid. Undoubtedly, contact angles reported in the literature sometimes deviate significantly from the Young’s angle for a variety of reasons.

The apparent variation of surface free energy with the choice of probe liquid sets undoubtedly, in part, results from physico-chemical interactions between solid and liquid that cause Young’s equation to be invalid for the present purposes. On the other hand, Kwok and Neumann have not always reported results from liquid sets containing diverse liquids. The mathematics of least squares fitting requires the use of a diverse set of liquids to achieve reliable values for the fitted parameters. Kwok, Li and Neumann [70, 53, 71] have also chosen a fitting procedure that allows 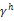 to be negative ( j = +, -) which appears contrary to van Oss’ statements (see Section 3.2). It is not clear, at this time, that the model proposed by Neumann and the model by van Oss, Chaudhury and Good are mutually exclusive as Neumann and co-workers suggest.

3.2.4 Fowkes approach [72,73,74] (Simple Fowkes and extended Fowkes)

This approach forms a basis of all the surface tension component approaches used today and the dispersion component of the total surface energy is still calculated by using this approach.

Fowkes considered the surface tension (γ) to be a measure of the attractive force between surface layer and liquid phase, and that such forces and their contribution to the free energy are additive. Therefore, the surface tension of liquid metals, polar liquids, hydrocarbons, low energy solids and other solids is considered to be made up of independent additive terms.

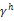           (1.57)He attrib

uted the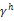term only to the London dispersion interactions because it has been shown for macroscopic condensed systems in aqueous media that out of the three electrodynamic interactions only London’s dispersion interaction is predominant [75,76]. 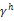 is due to hydrogen bonding and  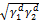due to metallic bonding, etc.

The intermolecular attractions, which cause surface tension, arise from a variety of well-known intermolecular forces. Most of these forces, such as metallic bonding and hydrogen bonding, are a function of specific chemical nature. However, London dispersion forces exist in all types of matters and always give an attractive force between adjacent atoms or molecules, no matter how dissimilar their nature may be. The London dispersion forces arise from the interaction of fluctuating electronic dipoles with the induced dipoles in neighboring atoms or molecules. The effects of fluctuating dipoles cancel out, but not that of the induced dipoles. These dispersion forces contribute to the cohesion in all substances and are independent of other intermolecular forces, but their magnitude depends on the  type of material and density. Therefore, the 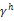  term includes only the London dispersion force contribution and, Keesom and Deby force contributions are included in the  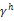 term.

The interface between two phases with only dispersion force interactions is composed of two monolayers as indicated in Fig. 18. At the interface, the adjacent layers of dissimilar molecules are in a different force field than the bulk phase and consequently, the molecules or atoms in these layers have a different pressure, intermolecular spacing and chemical potential. If the molecules in one of these monolayers are less strongly attracted by the adjacent phase than by its bulk phase, the molecules in the interfacial layer have an increased intermolecular distance and are in tension. However, if the attraction by the adjacent phase is greater than that of the bulk phase, the molecules of the interfacial monolayer have a shorter intermolecular distance and are under two-dimensional pressure. The measured tension of the interface is always the sum of the tensions in the two interfacial monolayers.

 

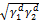
Fig. 1.18 Diagram of the two neighbouring monolayers at an interface in which tension resides. Taken From [51]

The surface monolayer of phase 1 has a tension γ₁ resulting from the unopposed attraction of the bulk liquid. An interfacial monolayer of phase 1 is attracted by its bulk in the identical manner, but this attraction is opposed by the attraction of phase 2. When the interacting forces are entirely dispersion forces (such as in between saturated hydrocarbons and water or mercury) then the decrease in tension in the interfacial monolayer of phase 1 resulting from the presence of phase 2 is 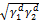 Consequently, the tension in the interfacial monolayer of phase 1 is - 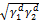 and in the interfacial monolayer of phase 2 is  which leads to the equation

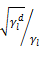             (1.58)

By measuring the interfacial tension at the saturated hydrocarbon/water interface and using the above equation, Fowkes calculated γ^d_water to be 21.8±0.7 mN/m, since only dispersive interactions between water and hydrocarbons exists. Similarly, he arrived at γ^d_Hg =200±7 mN/m by using a saturated hydrocarbon/mercury interface. Since mercury and water interacts only by dispersion forces, Fowkes was able to predict the interfacial tension to be 425±4 mN/m which agrees well with the experimental value of 426±4 mN/m for water/mercury interface. This demonstrates the usefulness of the geometric mean approach and helpful for both the liquid-liquid and liquid-solid interfaces.

At the solid-liquid interface the Fowkes relation looks as follows

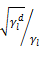     (1.59)

Combining this with the Young equation Eqn.1.2, we get an equation of the form:

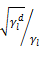        (1.60)

If the spreading pressure term, 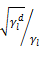 , is neglected then a plot of cosθ vs.  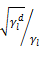gives a straight line (Fig. 1.19) with the origin at cos=-1 and slope 2  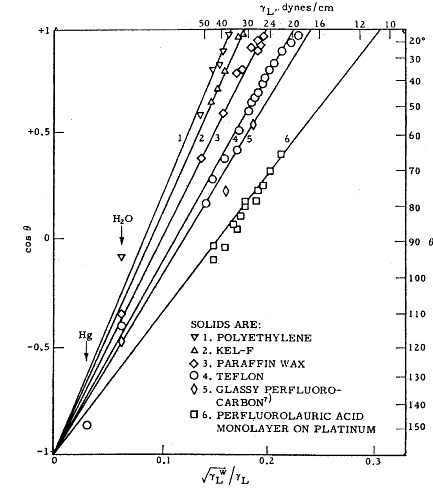 . Since the origin is fixed, one contact angle measurement is sufficient to determine the dispersion force component of the surface energy of the solid  .

The spreading pressure term, 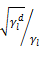  , can be assumed to be zero only for the system where high energy liquids are brought in contact with low energy solids. The basic reason for this assumption is that all theoretical and experimental evidence predicts that adsorption of high-energy materials cannot reduce the surface energy of a low energy material. For example, adsorbing water never reduces the surface tension of a liquid hydrocarbon.

The fact that a given liquid has a contact angle greater than 0° on a given low energy solid asserts that the liquid possesses a higher energy and therefore 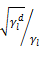 should be zero. This holds true only for the solids interacting by dispersion forces only. It does not apply for the high-energy solids such as metals, graphite; water does not wet these solids but it does absorb and produce appreciable .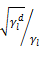

Based on just the thermodynamic point of view there are some objections on the usage of geometric mean to combine the dispersion force contribution of the two phases to arrive at the interfacial energy. Lyklema [77] put forward two reservations -whether it is thermodynamically allowable to split the interfacial tensions in components and secondly, if geometric mean is the most appropriate mathematical form to combine them? The first objection stems from the fact that the interfacial tensions are Helmholtz energies, whereas Fowkes _Eq. 1.48 approach treats them as energies. The entropy contributions are totally neglected and when entropy contributions are combined, they do not follow the geometric mean law but go with the logarithm of the composition.

Fig. 1.19  Relation of contact angle θ to surface tension of liquid γ_l

Except for the equation of state approach the Fowkes relation is used in all the surface tension component approaches to determine the dispersion (sometimes termed as ‘apolar’ and ‘Lifshitz van der Waals’) component of the total surface energy, Since this equation takes only apolar interaction into account, the contact angle data with an apolar liquid (e.g. methyleneiodide, α-bromonapthalene) must be used as this liquid would only have dispersion_van der Waals interaction with the bacterial cell surface.

Kitazaki and Hate [78] carried out the contact angle measurements with three series of liquids, A, B and C, for polyethylene and its four fluorine-substituted polymer.

It is based on the following assumptions which are formally extended from Fowkes' equation. 

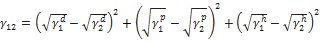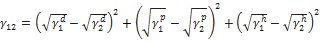,      (1.61)

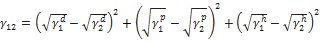     (1.62)

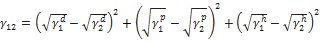     (1.62’)

where γ^d, γ^p and γ^h are components of surface tension γ, arising from dispersion force, polar (permanent and induced) force and hydrogen-bonding force respectively. γ^pand γ^h may be zero. Each parenthesis in Eq. (1.52)' is twice the difference between arithmetical and geometrical means, and therefore is negligibly small in the usual cases. Accordingly, when surface tensions of contacting materials both consist of the same kinds of components, in other words, in the cases of combinations of both nonpolar, both polar, and both hydrogen-bonding materials, their interfacial tension γ₁ becomes negligibly small. In this case, measured γ^h becomes maximum and is nearly equal to γ_s. On the other hand, when γ_l, for instance, lacks one or two components, which are included in γ₂, the component might contribute predominantly to γ₁₂, and give a smaller value of γ_c.

Extension of Fowkes' equation is merely formal, but has many advantages over the extended equation to two components proposed by Owens et and Kaelble et ai. It is useful particularly when we consider the wetting properties of solids for different liquid series d, p, and h, and when we want to estimate surface tension of solid.

3.2.5 Geometric mean equation (Owens-Wendt-kaelble approach)

Owens and Wendt [79] proposed the division of the total surface energy of a solid or liquid in two componentsdispersion force component and hydrogen bonding  component 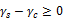 and 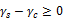 The interaction energy of the non-dispersive forces at the interface was quantified and included as geometric mean of the non-dispersive components of solid and liquid. The equation proposed was the extension of the equation proposed by Fowkes (Eq. 1.48)

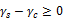             (1.63)

This can be alternatively expressed as 

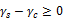       (1.63’)

The geometric mean combination of 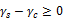 and 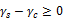 was used even though the fact that hydrogen bonding interactions are more specific in nature. The main reason was that the authors believed that hydrogen bonding is similar to the dipole-dipole interactions that take the form of a geometric mean.

Nearly at the same time, Kaelble [80] also published a very similar equation in terms of dispersion and polar force. Thus Eq. 1.63 if often called the Owen-Wendt-kaelble equation.

Owens and Wendt evaluated the surface energy of many polymers and then compared them to the values obtained by Zisman using the critical surface tension approach. A fairly good agreement was observed between the values from both the approaches. From Eq. 1.63’. it is apparent that 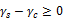. The following four cases follow and should be recognised:

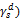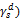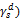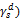- Use of non-polar liquid   to determine   of non-polar solids  Here  and 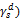  substituting these in Eq. 1.63’. we get  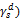, i.e. the critical surface tension gives the dispersion surface energy(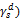. of the solid, which is equal to . γ_s

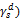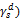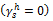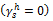- Use of non-polar liquid  to determine   of polar solids (Here and 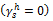  substituting this in Eq. 1.63’. we again get  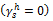, i.e. the critical surface tension gives only the dispersion part of the total surface free energy of the solid.

- Use of polar liquid to determine 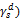   of non-polar solids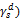. Here  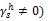 and 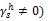  substituting these in Eq. 1.63’. we get 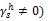this means that the use of polar liquids to determine  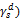   of non-polar solids leads to a value considerably less than γ_s  .

- Use of polar liquid 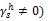   to determine  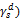  of polar solids(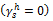. Here  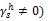and 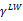  Substituting these values in Eq. 1.63’. we get  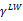which means that the use of polar liquids to determine  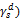  of polar solids leads to a value considerably less than γ_s.

3.2.6 Harmonic-mean and geometric-harmonic-mean equation (Wu 1,2)

Wu [81,82] proposed the harmonic mean to combine the polar and dispersion components of the solid and liquid surface energies in order to obtain the solidliquid interfacial energy and proposed the following expression:

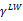         (1.64)

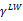     (1.65)

The first expression may be called the harmonic-mean equation preferred for low energy systems such as organic liquids, water, polymers, and organic pigments. The second may be called the geometric-harmonic-mean equation preferred for high energy systems such as mercury, glass, metal oxides and graphite.

Similar to the Geometric mean approach, the contact angle data with two liquids are required in order to obtain the polar and dispersion components of the solids surface energy.

3.2.7 Lifshitz-van der Waals (Van Oss-Chaudhury-Good method /Acid-base approach (LW-AB))

This approach came into existence when the thermodynamic nature of interface was re-examined by van Oss [83] in the light of Lifshitz theory of forces. The role of van der Waals forces and hydrogen bonds was studied in order to explain the strong attachment of biopolymers Žhuman serum albumin, human immunoglobulin. on low energy solids Žpolytetrafluoroethylene, polystyrene. which was previously attributed to the hydrophobic interactions.

This idea of the partition of the SFE of solids and liquids into components is that presented by van Oss, Chaudhury, and Good [83,84]. The authors divided γ_s into two components, one including the long-range interactions (London, Keesom, and Debye), called the Lifshitz-van der Waals component ( 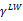) , and the other that contains the short-range interactions (acid-base), called the acid-base component (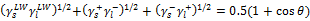)    . The latter component is considered to be equal  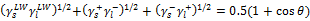 , where 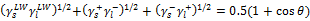and 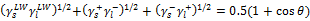 mean the acidic and basic constituents, respectively, which are associated with the acid-base interactions. As a result, the following relationship was formulated: 

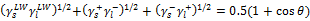      (1.66)

Derivation of Eq. 16 has been initiated by the results of the studies on interactions between proteins (biopolymers) and hydrophobic solids and by the attempts to explain the then unclear term a hydrophobic bond [83].

Taking into account that the component 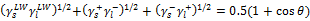is equal  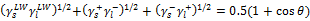and combining Eq. 1.2 with Eq. 1.56, van Oss, Chaudhury, and Good obtained the following relationship [84]:

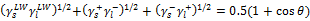                 (1.67)

Since three unknowns,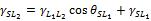, 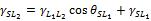and 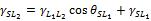, appear in Eq. 1.67. Such a system is obtained when three different liquids are used to measure the contact angle of a studied polymeric material. One nonpolar and two bipolar liquids should constitute the set of the three measuring liquids. The values of the coefficients appearing in such a system of equations, for several sets of these liquids, have been given elsewhere [85].

The solution of the system of three equations represented by Eq.1.67, as used in the van Oss-Chaudhury-Good method, cannot always be proper and unequivocally interpreted. This follows from the assumed conditions and limitations, associated with both the kinds of selected measuring liquids and the ways of determination of the SFE components such as 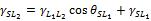, 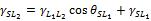and .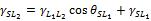

The effect of wrong conditions relating to the system of linear equations on its solution may be discussed considering the following example. The solution of the system of two linear equations, x + 20y = 21 and 2x + 41y = 43, consists in a pair of numbers, x = 1 and y = 1. If the coefficient at ‘y’ in the first equation is changed from 20 to 19.99 (i.e., by 0.05%), then the pair of numbers, x 􀂧 1.41 and y ≈0.98, is the solution of a new system of equations, x + 19.99y = 21 and 2x + 41y = 43. It means that a very small change in the value of only one coefficient may cause many times larger changes in the solution (‘x’ increases by ca. 41% and ‘y’ decreases by ca. 2%). If four coefficients in the two equations are changed, each by 0.01, then a new system of equations, x + 19.99y = 21.01 and 2x + 41.01y = 42.99, is obtained, the solution of which consists in a pair of numbers, x = 2.18 and y =0.94. In this case, very small changes in the values of the coefficients (by 0.05, 0.0476, 0.0244, and 0.0233%, respectively) cause very large changes in the solution (‘x’ increases by ca. 118% and ‘y’ decreases by ca. 6%).

When the values of the coefficients at the unknowns in an improperly conditioned system of linear equations are determined from independent measurements and calculations, then an even very small measurement or calculation error of only one of these values may totally distort the solution (see the first part of the example above). Also, the measurement or calculation errors made during the determination of the remaining coefficients at the unknowns as well as the experimental errors relating to the values of the coefficients that appear on the right-hand side of the transformed equations represented by Eq. 1.57, may cause the obtained solution to be inconsistent with the current state of knowledge and with the expected result. It means that this solution may be wrong. Proper conditions relating to the system of equations represented by Eq. 1.57 are secured by, e.g., the following sets of liquids: WGD, WFD, and GFB.

The argument is that often, the polar (Keesom and Debye) forces are weak, and can be included in the dispersive contribution. The “combined” contribution is denoted by LW –Lifschitz-van der Waals. In addition, there is a short-range interaction (SR) that is caused byacid-base interactions (hydrogen bonding is a type of acid-base).

A detailed discussion on the above conditions and limitations has been presented elsewhere [86]. The van Oss-Chaudhury-Good method is undoubtedly one of the recent achievements in the studies on the SFE of polymeric materials. In spite of many disputes and controversies over the results obtained by this method, it enables to learn better the examined phenomena, especially the interfacial acid-base interactions.

3.2.8 Measurements of high energy surfaces (Schultz1,2)

As most liquids are spread on a high energy surface, the contact angle cannot be measured. However, Schultz (1977) [87] has developed a method where these angles may be measured by submerging the surface in one liquid and using a second liquid to measure the contact angle. This method is generally called two-liquid-phase contact measurement. Systems involving water in dydrocabon media are usually chosen, usually, hydrocarbons like n-hexane, n-octane, n-decane, and n-hexadecane are used as the surrounding liquids and water as the contact angle liquid. It is also possible to apply the two-liquid-phase method to low-energy solid as described by author [87].

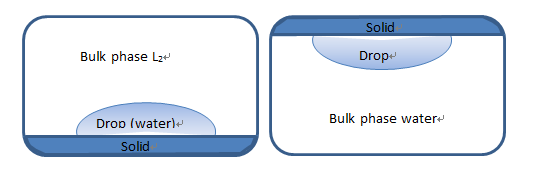
An important contribution for determining surface properties of high-energy solids by mean of the two-liquid-phase method was done by Schultz and coworkers.[88,89]. Fig 1.20 shows a schematic representation of two-liquid-phase contact angle system. Assuming that Young’s equation can be applied to a liquid L1-liquid L2 (bulk phase) – solid S system, the following relationship can be obtained:

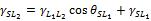          (1.68)

where 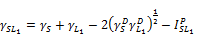, 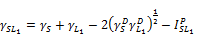and 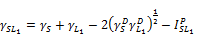 are , respectively, the interfacial free energies of S-L₂, L₁-L₂, and S-L₁ interfaces, and  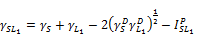 is the contact angle of a drop of liquid L₁ on solid S. It is seen that 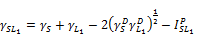, which could be considered as the driving force of spreading in the one-liquid phase method, is replaced by γ_SL2 , which is generally smaller than . This leads to a finite and thus measureable value of contact angle. According to Fowkes theory (As described upper),  γ_SL1 and  γ_SL2  are given by  :

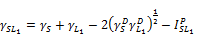    (1.69)

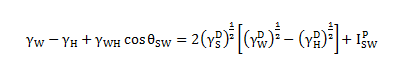    (1.70)

Where γ and γ^D are the surface energy and its dispersive component, respectively, and 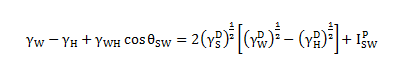  is a specific (or non-dispersive) interaction term that includes all the interactions established between the solid S and the liquid L (dipole-dipole, dipole-induced dipole, hydrogen bonds, Π bonds, …) except London dispersion interactions.

Substituting Eqn. 1.69 and 1.70 into 1.58 leads to 

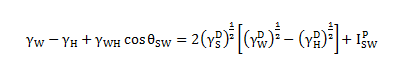    (1.71)

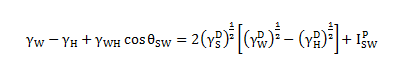
Fig. 1.20  Schematic representation of a two-liquid-phase contact angle

If liquid L₁ is water (subscript W) and liquid L₂ is an n-alkane (subscript H), the term 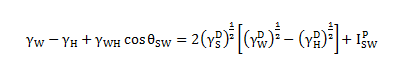   may be considered equal to zero since the surface free energy of n-alkane consists only London dispersion term. Finally, Eq. 1.71 can be rewritten as 

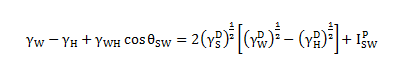     (1.72)

And Eq. 1.72 is always named as Shultz 1.

The polar part of  can be calculated by applying Fowkes theory:

                                                    (1.73)

This method therefore allows the determination of the dispersive component of the surface energy of the solid, , as well as the magnitude of the non-dispersive interactions between water and solid surface.

Nevertheless, this principle is based on the assumption that a droplet of water can displace the alkane layer from the solid surface at contact. It is not certain to what extent this will happen and that there will not remain a thin film of the non-polar liquid between the solid and water, thus preventing direct contact. Therefore, it is necessary to define a criterion for displacement.

Schultz 2 is a method similar Schultz 1 with the difference that the L₁ is non-polar (such as water) and L₂ (surrounding liquid) is polar. The calculations are carried out using Eq. 1.71, and 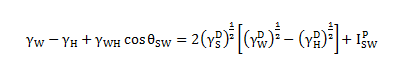    needs to be involved in calculation by using polar energy of L₂. We note that drop type of Schultz 2 is captive drop method due to non-polar liquid will be floated, as shown below:

Fig. 1.21 Drop type for Schultz method, left is sessile drop for Schultz 1 and right is captive drop for Schultz2

3.2.9 Contact angle Hysteesis (CAH) (Chibowski method) [101]

Recently Chibowski [90,91-93] derived an equation for total surface free energy of a solid from advancing θ_a and receding θ_r contact angles of only one probe liquid:

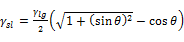                  (1.74)

Thus the evaluated surface free energy of a given solid depends, to some extent, on the kind of probe liquid used. However, if several probe liquids are used the averaged value (arithmetic mean) of the solid surface free energy agrees perfectly with the mean value of total surface free energy determined from LWAB approach if several triads of probe liquids are used for the contact angle measurements and the calculations [92]. If one considers that the equilibrium contact angle θe is that when no hysteresis appears, i.e. θa =θr =θe  then from equation 1.74 , it result that [93]:

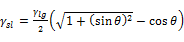               (1.75)

With this assumption, if the equilibrium contact angle of this liquid is known indeed, the solid surface free energy equals half of the work of adhesion of this probe liquid to the solid surface [93].

In the derivations of this model no assumption has been done as for the film state. It was only assumed that retreat the contact line of liquid drop the solid surface could not be left completely bare, because at least the London dispersion interactions are present. The more in real systems, where solid surface practically always possesses some imperfections (micro heterogeneity) and roughness. Some amount of the liquid will be left behind the drop, which forms the film. If this model works, total surface free energy of a solid can be evaluated from three measurable parameters, i.e. probe liquid surface tension and its advancing and receding contact angles measured on the investigated solid surface [91, 94]. It may be WARNINGd that Eq. (1.65) works also for zero receding contact angle (cosθ=1), but it has a limitation when no hysteresis appears (formally for θa=θr). However, even for a very low energy solids contact angle hysteresis appears [95-98] and this equation still gives very reasonable values for the solid surface free energy [92,94]. Some extreme cases of Eq. (1.65) were analyzed elsewhere [94]. It is also worth mentioning that in physicochemical sense also Young’s equation has limitation for zero-contact-angle and cannot be employed for a completely spreading liquid. Such liquid does not form any contact angle and not the zero contact angles. This possesses an essential mathematical differentiation. The model will be now tested using exact data of the advancing and receding contact angles taken from Lam et al. [99,100].

3.2.10 Jhu method  [102]

In 2007, Jhu and his coworkers developed a series of equation that also derived from Eq. 1.2, as shown below:

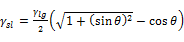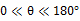 ,            (1.76)

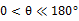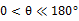,           (1.77)

Where γ_sg is surface free energy between solid and gas, γ_sl is interface free energy between solid and liquid and γ_lg is surface tension of liquid. Surface free energy can be calculated by one probe liquid also.

3.2.11 Summarizing table

In the following table, all methods used together with their characteristics and requirements are listed.

Method	Information	Min. no. of liquids	Application	Examples
Zisman	Critical surface tension	2	Non-polar solids	PE, PTFE, waxes
Fowkes	Disperse parts of surface free energy	2, non-polar liquids	Non-polar system	PE, PTFE, waxes
OWRK	Disperse and polar parts	2	universal	Polymers, aluminum, coating, vanishes
Extended Fowkes	Disperse, polar and hydrogen parts of surface free energy	3	Specific questions of surface properties	Plasma, or corona treated polymers
Wu1 (Harmonic Mean )	Disperse and polar parts of surface free energy	2, at least one polar liquid	Low energetic systems	Organic solutions, polymers, organic pigments
Wu2 (Geometric-harmonic-mean)	Disperse and polar parts of surface free energy	2, at least one polar liquid	High energetic system	aluminum, glass
Acid-Base Theory	Disperse, acid and base parts of surface free energy	3	Specific questions of surface properties	Biological system
Schultz1,2	Disperse and polar parts of surface free energy	2, at least one polar liquid	High or low energetic system	Polymers, aluminum, coating, vanishes
Good-and Garifalco approach	surface free energy	1	Low energetic systems	Organic solutions, polymers, organic pigments
Equation of State Theory	surface free energy	1	universal	Polymers, aluminum, coating, vanishes
Chibowski method	surface free energy	1	universal	Polymers, aluminum, coating, vanishes
Jhu method	surface free energy	1	universal	Polymers, aluminum, coating, vanishes